티스토리 뷰

문제
계단 오르기 게임은 아래와 같은 규칙이 있습니다.
- 계단은 한 번에 한 계단 또는 두 계단씩 오를 수 있다.
- 연속된 세개의 계단을 모두 밟아서는 안된다. 단, 시작점은 계단에 포함되지 않는다.
- 마지막 도착 계단은 반드시 밟아야한다.

출처 : https://www.acmicpc.net/problem/2579
입, 출력
입력
첫째 줄에 계단의 개수(N)가 주어집니다.
둘째 줄부터 한 줄에 하나씩 제일 아래에 놓인 계단부터 순서대로 각 계단에 점수가 부여됩니다.
계단의 개수 N개는 300이하이고, 계단에 쓰여 있는 점수는 10,000이하입니다.
출력
계단 오르기 게임에서 얻을 수 있는 총 점수의 최댓값을 출력합니다.
// 입력
6
10
20
15
25
10
20
// 출력
75
풀이 (설명)
최댓값 공식 찾기
한 계단 또는 두 계단씩 오를 수 있으므로 마지막 계단에 도착하기 위해서는 N-2번째 계단, N-1번째 계단에 있어야합니니다.
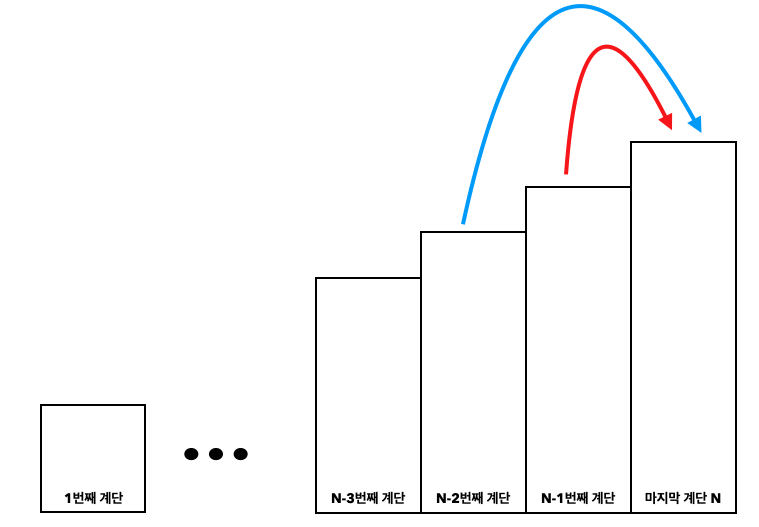
이렇게 본다면 마지막 N번째 계단은 N-2번째 N-1번째 계단이전에 한계단씩 올라왔는지 두계단씩 올라왔는지 모릅니다.

그래서 마지막 계단을 밟을 때는 두가지의 경우로만 공식을 세웁니다.
- 마지막 계단을 두 계단으로 올라 왔을 때
- 마지막 계단을 한 계단으로 올라 왔을 때
- 조건에 계단을 연속인 3개의 계단을 밟을 수 없다고 하였습니다.
- 근데 이전 계단에도 한계단으로 올라 올 수 있는 경우도 있기 때문에 N-3번째 계단에서 두 계단을 오르고 N-1계단에서 마지막 계단을 한 계단으로 올라오는 루트를 잡았습니다.
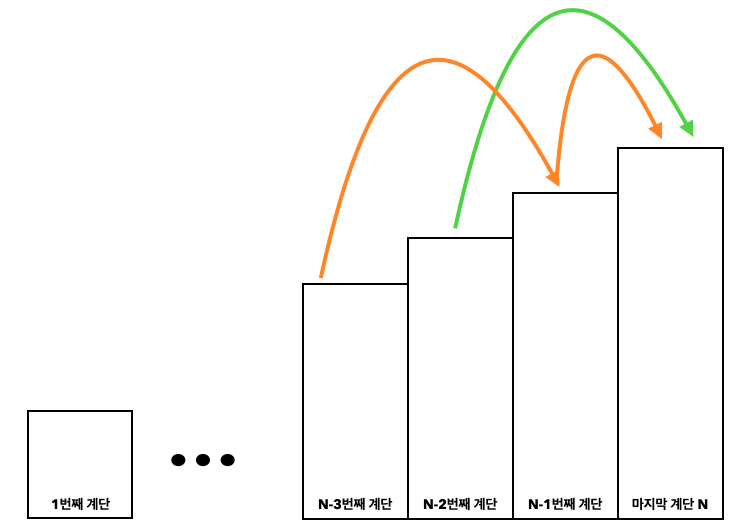
알고리즘 공식 작성
이제 간단히 생각을 해보면 됩니다.
- 마지막 계단에 오르기전 N-2번 째 계단, N-1번 째 계단의 최대 값은?
- 그럼 N-2번째 계단과 N-1번째 계단도 같은 공식을 사용?
- 같은 공식을 써서 Top-Down형식으로 찾아?
- !! 재귀?
// 최대값을 찾는 함수 step
function step(int n) { ... }
// 계단 점수를 넣을 배열
int[] score = new int[N+1];
// 마지막 계단을 두 계단으로 올라 왔을 때 최댓값
step(N-2)
// 마지막 계단을 한 계단으로 올라 왔을 때 최댓값
// 추가설명 : (N-3번째 계단에서 최대 값 찾고 N-1번째 계단으로 반드시 오므로)
step(N-3) + score[N-1]
// 결론 = 이전계단 최대 값 + 마지막오른 계단 점수 값
Math.max( step(N-2), step(N-3) + score[N-1] ) + score[N]
주의사항
계단이 -1계단 -2계단이라는 것은 없을 것입니다.
N-3번째 계단의 최댓 값을 갖기 위해서는 계단이 3개이상 있을 때 부터 가능한 공식이라는 것입니다.
그럼 계단 1개만 있을 때는? 첫번째 계단 점수만 출력하면 될 것입니다.
그럼 계단 2개만 있을 때는? 첫번째 계단 점수 + 두번째 계단 점수를 출력하면 될 것입니다.
같은 계산을 계속 반복하면 동적프로그래밍으로!
계단 최댓값을 찾을 때 재귀를 통해 같은 계산을 계속 반복하면 엄청 느려질 수 밖에 없습니다.
따라서, 같은 계산을 반복하는 것은 동적프로그래밍의 알고리즘 처럼 계산한 것을 어딘가에 담아두고 그것을 이어서 이용하는 방법을 이용하면 성능이 크게 향상됩니다.
풀이 (코드)
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
public class Main {
static int N; // 계단의 개수
static int[] scores; // 각 계단의 점수
static int[] DP; // 중복 계산 안하기 위한 DP 배열
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
N = Integer.parseInt(br.readLine());
scores = new int[N+1];
DP = new int[N+1];
// 데이터 넣기
for(int i = 1; i <= N; i++) {
scores[i] = Integer.parseInt(br.readLine());
}
System.out.println(step(N));
}
// Top-Down으로 값 찾기
public static int step(int n) {
if (n <= 0) {
return 0;
}
if (n == 1) {
DP[1] = scores[1];
return DP[1];
}
if (n == 2) {
DP[2] = scores[1] + scores[2];
return DP[2];
}
// 이미 연산된 작업이면 그 값 리턴
if (DP[n] != 0) {
return DP[n];
}
// 최댓값 찾기 !
DP[n] = Math.max(step(n-2), step(n-3) + scores[n-1]) + scores[n];
return DP[n];
}
}

감사합니다.
'코딩 테스트 > 🪙백준' 카테고리의 다른 글
| [백준] 31575번 도시와 비트코인 : BFS vs DP(동적계획법) 어떤 게 더 빠를까? (0) | 2025.12.23 |
|---|---|
| [백준] 25418번 A → K 최단 거리 구하기: BFS vs 역방향 그리디 (0) | 2025.12.20 |
| [백준] 15649번 N과 M (1) - JAVA (1) | 2024.04.19 |
| [백준] 2447번 별찍기 10 - JAVA (0) | 2024.04.15 |
| [백준] 11729번 하노이 탑 이동 순서 - JAVA (0) | 2024.03.11 |
- Total
- Today
- Yesterday
- 디자인패턴
- BFS
- JavaScript
- Front
- 개발환경
- Spring Security
- 실시간 채팅
- 멀티모듈
- 데이터 베이스
- 네트워크
- 개발
- 그리디
- Fetch
- 트랜잭션
- 계단 오르기
- 프로세스
- JPA 페이징
- 코딩테스트
- 개발블로그
- 카카오 로그인
- java
- 개발자
- Flutter
- 깃허브 액션
- DBeaver
- 시간 객체
- 알고리즘
- aws
- 소셜로그인
- spring
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
